Mathematics and Planet Earth: an interview with Valerio Lucarini MAE#
Newly-elected MAE Valerio Lucarini explains the role of mathematics in climate science, the importance of interdisciplinary research collaboration and the need to engage with policymakers.
About Valerio Lucarini MAE#
Valerio Lucarini is Professor of Statistical Mechanics and directs the Centre for the Mathematics of Planet Earth at the University of Reading (UK). Having led interdisciplinary research between mathematics and climate science over many years, his research has been recognised through a number of awards. They include the 2018 LMS Whitehead Prize for his work applying the ideas and methods of statistical physics to the theory and modelling of climate dynamics, and for his leadership in the field of mathematics applied to climate science, the 2020 Lewis Fry Richardson Medal for outstanding work on better understanding changes in the global climate, and the 2022 SIAM Activity Group on Mathematics of Planet Earth Career Prize for his research applying mathematical analysis to climate predictions. Professor Lucarini was also the recipient of the 2021 Ed Lorenz Lecture, in the Nonlinear Geophysics Section of the American Geosciences Union (AGU) Honors 2021 for his work in using mathematics to attempt to identify tipping points in the Earth’s climate system. He was elected to the Academia Europaea in 2022.
The interview#
Valerio, congratulations on your election to the Academia Europaea. What does it mean to you?
Tell us a little about your career path and outcomes. Who would you say were the people who have had the greatest impact on your work and career? Do you have any particular career highlights or achievements of which you are particularly proud?
 . At the time I was mainly interested in condensed matter physics. After a while I realised that I really wanted to delve into themes associated with the environment and with complexity, hence I pursued graduate studies in climate science at MIT, under the supervision of P. Stone
. At the time I was mainly interested in condensed matter physics. After a while I realised that I really wanted to delve into themes associated with the environment and with complexity, hence I pursued graduate studies in climate science at MIT, under the supervision of P. Stone . As a result of very unfortunate circumstances, I decided to leave after a couple of years and come back to Europe. Here I was rescued by K-E. Peiponen
. As a result of very unfortunate circumstances, I decided to leave after a couple of years and come back to Europe. Here I was rescued by K-E. Peiponen , who suggested that I complete my graduate studies in Finland at the University of Joensuu (now of Eastern Finland), where I got my PhD in nonlinear optics, while, at the same time, bringing forward my research and studies in climate science. Professor Peiponen believed in me at a moment of great difficulty, and I will always be incredibly grateful to him for this. My wonderful Finnish adventure led to a book on Kramers-Kronig relations for optical materials co-authored by me, K.-E. Peiponen, J. Saarinen (another PhD student), and E. Vartiainen. Undoubtedly, this was my first scientific milestone. After that, I switched to climate studies and worked in collaboration with A. Speranza
, who suggested that I complete my graduate studies in Finland at the University of Joensuu (now of Eastern Finland), where I got my PhD in nonlinear optics, while, at the same time, bringing forward my research and studies in climate science. Professor Peiponen believed in me at a moment of great difficulty, and I will always be incredibly grateful to him for this. My wonderful Finnish adventure led to a book on Kramers-Kronig relations for optical materials co-authored by me, K.-E. Peiponen, J. Saarinen (another PhD student), and E. Vartiainen. Undoubtedly, this was my first scientific milestone. After that, I switched to climate studies and worked in collaboration with A. Speranza , who had a great influence in encouraging me to find my own way in the rapidly evolving scholarship of climate science.
, who had a great influence in encouraging me to find my own way in the rapidly evolving scholarship of climate science.
In 2007 I obtained a permanent academic position at the University of Bologna. I then moved to Reading. In 2011, after obtaining an ERC Starting Grant on the Thermodynamics and Statistical Mechanics of Climate, I was offered a professorship at the University of Hamburg, where I led the group of Theoretical Meteorology. In these years, I started developing my own scientific vision of climate as a nonequilibrium system, to be investigated through the lens of thermodynamics and statistical mechanics and using models of different level of complexity. K. Fraedrich
 , G. Gallavotti
, G. Gallavotti , M. Ghil
, M. Ghil , J. Lebowitz
, J. Lebowitz and D. Ruelle
and D. Ruelle have been very influential over the years. The main scientific achievements during this period have been the idea of using response theory for developing flexible climate change projections (and here my condensed matter physics background was key to foreseeing this research direction); the provision of a coherent framework for describing the climate as a thermal engine; and the development of a mathematical theory of extreme events, specifically aimed at studying geophysical extremes. The development of such a theory required a broad and interdisciplinary team working across geosciences, physics and mathematics. I am very proud of this collaboration, which led to the write-up of an appreciated monograph. I am even more proud of the fact that my first PhD student, D. Faranda
have been very influential over the years. The main scientific achievements during this period have been the idea of using response theory for developing flexible climate change projections (and here my condensed matter physics background was key to foreseeing this research direction); the provision of a coherent framework for describing the climate as a thermal engine; and the development of a mathematical theory of extreme events, specifically aimed at studying geophysical extremes. The development of such a theory required a broad and interdisciplinary team working across geosciences, physics and mathematics. I am very proud of this collaboration, which led to the write-up of an appreciated monograph. I am even more proud of the fact that my first PhD student, D. Faranda , who is an extremely accomplished scientist and a dear friend, had the intellectual depth and the intuition to envision applications for our theory that I would have never dreamed of. Also, in this period, I dedicated a lot of time to fostering international cooperation with institutions in South Asia, China, and Russia. I have wonderful memories, at a personal and professional level, of these activities.
, who is an extremely accomplished scientist and a dear friend, had the intellectual depth and the intuition to envision applications for our theory that I would have never dreamed of. Also, in this period, I dedicated a lot of time to fostering international cooperation with institutions in South Asia, China, and Russia. I have wonderful memories, at a personal and professional level, of these activities.
After 2017 I moved back to the UK and took up a professorship in statistical mechanics at the University of Reading, where I have founded, and am still directing the Centre for the Mathematics of Planet Earth
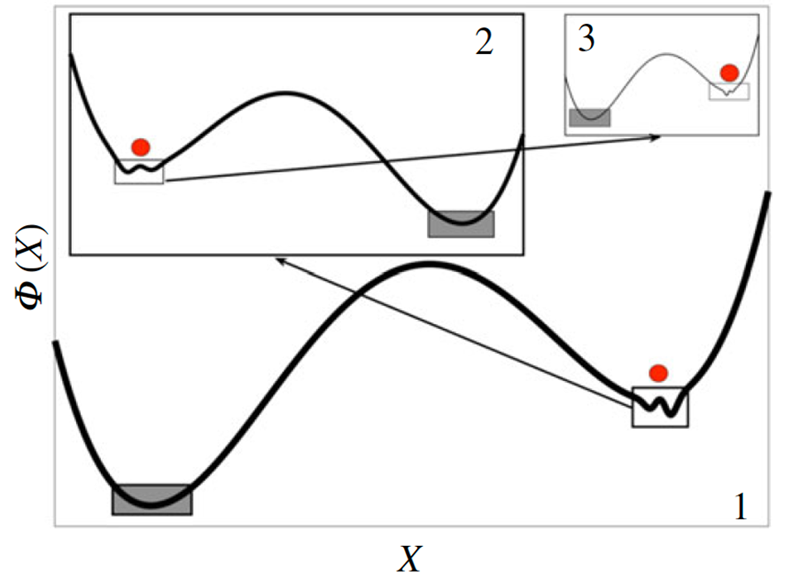
 . In these last few years, my research has mostly focused on the development of a mathematical framework for studying climatic tipping points and the metastability properties of the Earth system. I am now involved in two very stimulating European projects – TiPES
. In these last few years, my research has mostly focused on the development of a mathematical framework for studying climatic tipping points and the metastability properties of the Earth system. I am now involved in two very stimulating European projects – TiPES and CriticalEarth
and CriticalEarth – dedicated to these themes. I am very happy with the results I have obtained in close collaboration with T. Bodai
– dedicated to these themes. I am very happy with the results I have obtained in close collaboration with T. Bodai , M. Chekroun
, M. Chekroun , V. M. Galfi
, V. M. Galfi , A. Gritsun
, A. Gritsun , A. Tantet
, A. Tantet and J. Wouters
and J. Wouters and very grateful to the late B. Eckhardt
and very grateful to the late B. Eckhardt and to J. Yorke
and to J. Yorke for their continuous encouragement. A funny note: I had a key intuition while watching the movie Melancholia by L. von Trier – hence I named as “Melancholia states” those unstable states responsible for the multistability of the Earth system.
for their continuous encouragement. A funny note: I had a key intuition while watching the movie Melancholia by L. von Trier – hence I named as “Melancholia states” those unstable states responsible for the multistability of the Earth system.
Let me stress that I feel very, very indebted – personally and professionally – to my graduate students and to my post-doctoral collaborators. It is really hard to find the right words.”
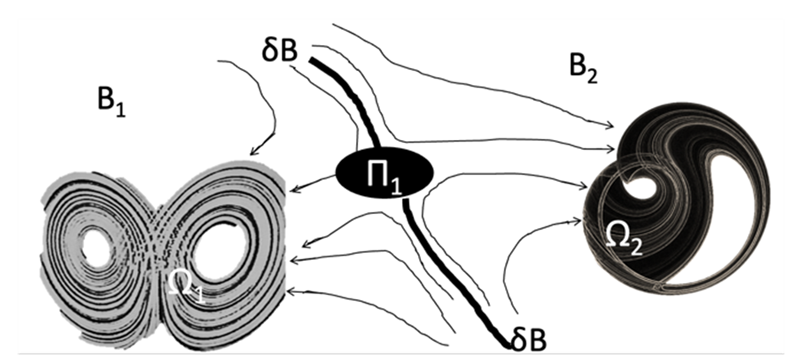

You have been leading work that combines mathematics with climate science. Can you give us the highlights of your research findings? What contribution can your research make to facing the challenges of climate change? Do you see your research having an impact on policy?
Additionally, I believe that our research results on meteo-climatic extremes could have important societal implications. Our theoretical framework is based on the theories of extreme value and dynamical systems; it allows one to better estimate and constrain the return times of extreme events from the data, which one can then model and assess the impact of climate on extremes. More recent work on extremes, based on large deviation theory, is particularly well-suited for studying persistent temperature anomalies – heatwaves and cold spells – and possibly – we are still looking into that – drought or certain classes of flood events. Also in this case, the idea is to look for some sort of universality in the statistical properties of extreme events, and then exploit it to have predictive power on the probability of occurrence of yet unobserved events and to better understand the dynamical processes leading to the extreme event of interest. Many of the results we have presented could find applications in many other areas of complexity science – extreme events are often conducive to risks, so it is important to be able to better understand and anticipate them.”

Where is your research going next? What are your priorities?
The interview was conducted by the Academia Europaea Cardiff Knowledge Hub
 .
.


